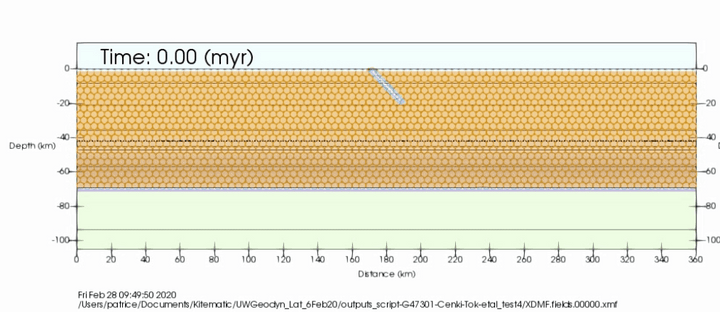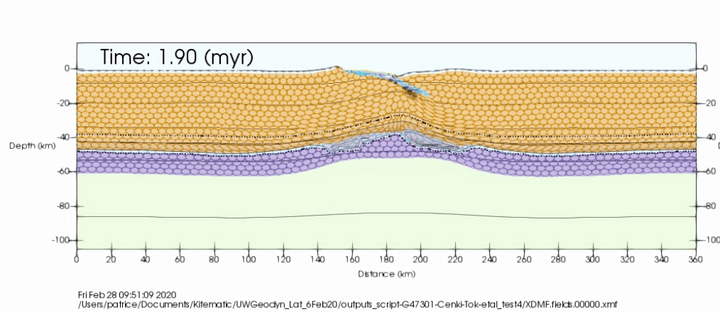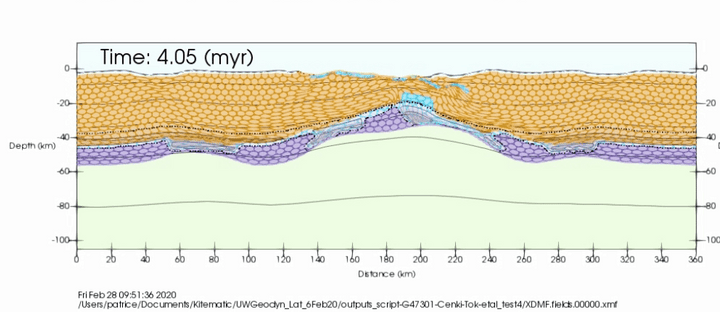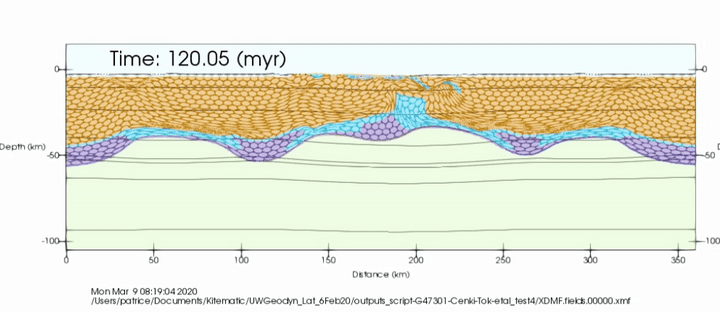
Underworld Geodynamic Modelling Workshop. Perth, 7 May 2025
You are invited to a full-day workshop on Underworld — a computational Geodynamics / Tectonics modelling framework. This is an excellent opportunity for researchers, students, and professionals interested in computational geodynamics and Earth science modelling to learn about Underworld.