Stripy
A Python module for (constrained) triangulation in Cartesian coordinates and on a sphere.

The triangulation of scattered points is a common problem in science and engineering when local neighbourhood information is required for computation. Typical applications include the calculation of neighbour relationships, interpolants, derivatives, and smoothly-fitting surfaces. A more specialised problem is the triangulation of points distributed on the surface of a sphere, nevertheless, this is important in most global geographical applications where data are registered in longitude and latitude and the Earth's ellipticity can be considered as a second order effect.
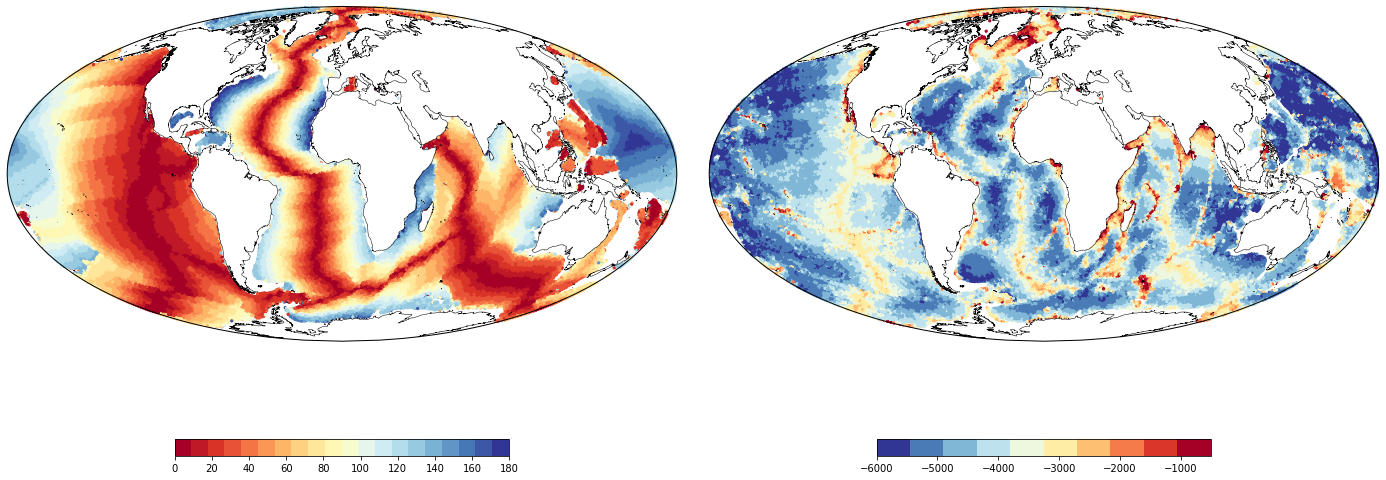
Stripy is a numpy-based interface to TRIPACK and STRIPACK Fortran code for (constrained) triangulation in Cartesian coordinates and on a sphere, respectively (Renka 1996a,b and 1997a,b). Our focus in developing an augmented set of wrappers for a venerable and widely used set of fortran subroutines has been on ease of use so that triangulated or scattered data on the sphere can be brought quickly into interactive jupyter notebooks for analysis and interrogation.
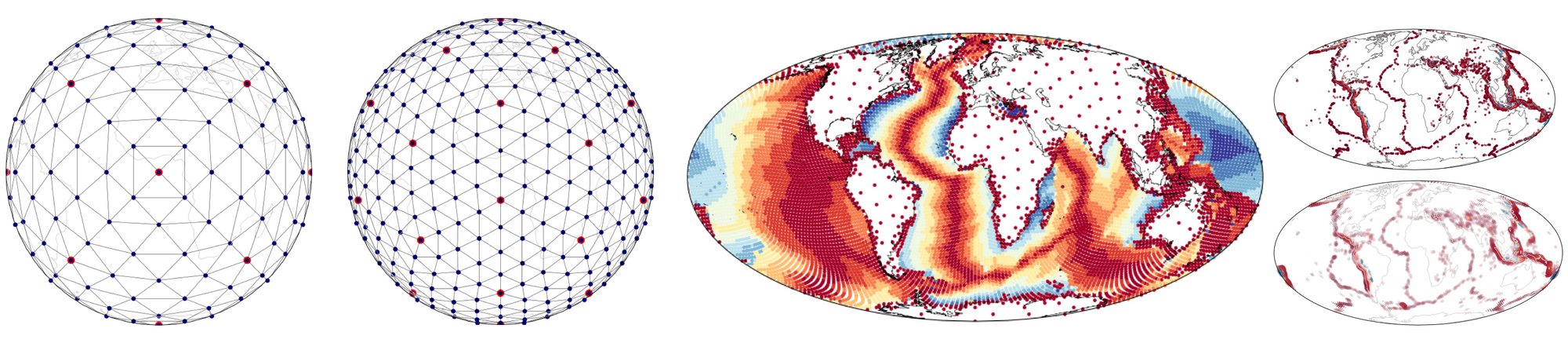
Stripy is an object-oriented package that extends the functionality of the original collection of subroutine by adding a number of useful tools such as the construction of regular meshes on the sphere (icosahedral and octahedral each with face-centre-point variants, a triangulated cube and a truncated icosahedron with face-centre points that produces a C60 / soccerball mesh). Stripy also includes functionality to refine meshes globally and locally by triangle or edge subdivision. We have taken some care to ensure that queries on the triangulations are vectorised within numpy queries. Stripy offers a consistent API between the two coordinate system so users can transfer from Cartesian to spherical coordinates with minor changes to their code.
What Stripy can do:
- Spherical and Cartesian (Delaunay) triangulation of scattered points.
- Building the Voronoi Diagram for triangulations.
- Construction of Cartesian and Spherical meshes.
- Nearest-neighbour, linear, and hermite cubic interpolation with user-configurable spline tensions.
- Evaluation of derivatives.
- Smoothing operations.
- Mesh refinement on line segments / triangle centroids.
- Fast point location with k-d tree interface with angular separation metric on the sphere.
Documentation
Stripy is bundled with a linked collection of jupyter notebooks that can act as a user guide and an introduction to the package. The notebooks are split into matching sets for spherical and Cartesian triangulations. Head to the Stripy GitHub Repository to browse the code and API documentation or launch the demo using Binder:
Installation
We offer Docker images, PyPI and Conda packages to get you started with Stripy. Installation with pip:
pip install stripyThis may require you to have a Fortran compiler, such as gfortran, installed on your system. Alternatively, installation with Conda has the required binary files and can be accessed via the underworldcode channel:
conda install -c underworldcode stripyWe also offer a Docker image bundled with dependencies and Jupyter notebook examples:
docker pull underworldcode/stripy:latest
docker run underworldcode/stripy:latestHow to cite Stripy:
Moresi, L. and Mather, B.R., (2019). Stripy: A Python module for (constrained) triangulation in Cartesian coordinates and on a sphere. Journal of Open Source Software, 4(38), 1410, https://doi.org/10.21105/joss.01410
References
- Laske, G., G. Masters, and Z. Ma (2013), Update on CRUST1. 0—A 1-degree global model of Earth's crust, Geophys Research Abstracts, 15, EGU2013–2658.
- Pasyanos, M. E., T. G. Masters, G. Laske, and Z. Ma (2014), LITHO1.0: An updated crust and lithospheric model of the Earth, Journal of Geophysical Research-Solid Earth, 119(3), 2153–2173, doi:10.1002/2013JB010626.
- R. J. Renka, "ALGORITHM 751: TRIPACK: A Constrained Two- Dimensional Delaunay Triangulation Package" ACM Trans. Math. Software, Vol. 22, No. 1, 1996, pp. 1-8.
- R. J. Renka, "ALGORITHM 752: SRFPACK: Software for Scattered Data Fitting with a Constrained Surface under Tension", ACM Trans. Math. Software, Vol. 22, No. 1, 1996, pp. 9-17.
- R. J. Renka, "ALGORITHM 772: STRIPACK: Delaunay Triangulation and Voronoi Diagram on the Surface of a Sphere" ACM Trans. Math. Software, Vol. 23, No. 3, 1997, pp. 416-434.
- R. J. Renka, "ALGORITHM 773: SSRFPACK: Interpolation of Scattered Data on the Surface of a Sphere with a Surface under Tension", ACM Trans. Math. Software, Vol. 23, No. 3, 1997, pp. 437-439.
