Free surface in Underworld

Free surface in geodynamics simulations
Geodynamic simulations increasingly rely on models with a true free surface to investigate questions of tectonic deformation, mantle convection, and coupling of surface processes and lithosphere dynamics. Historically, most mantle convection simulations have been performed with free-slip boundary conditions at the surface. However, the Earth's surface is a free surface, which implies that both normal and shear stress should be zero at this interface. Moreover, it has been shown that treating the Earth's surface as a free surface can have a significant effect on lithospheric and mantle dynamics (Schmeling et al., 2008; Kaus et al., 2010).
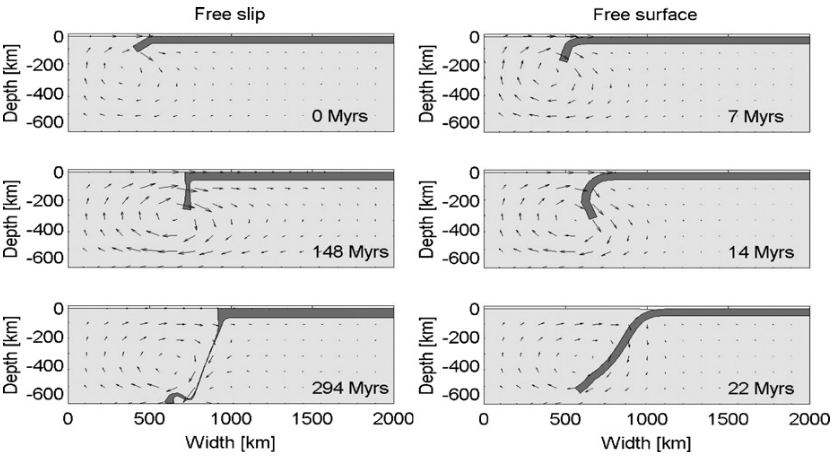
Free subduction experiment in which a linear viscous slab sinks into a linear viscous mantle (Kaus et al., 2010).
Approaches for treating the free surface
There have been several approaches to simulate real free surfaces in geodynamic models:
(1) Body-fitting method (or conforming mesh based method). This method enables the mesh to conform with the topography, a zero normal stress condition can then naturally be applied on the surface. Such configuration employs either a deforming Lagrangian grid or an Arbitrary Lagrangian-Eulerian (ALE) framework.
(2) Another kind of method employs an Eulerian mesh. The Marker-and-Cell method, level-set functions, or hybrid methods are commonly used here. Free-surface tracking techniques allow for the identification of the cells in the flow grid that contain the interface, which allows a free-surface boundary condition to be applied to the interface cells within the grid.
(3) "Sticky air" method (for a comprehensive review see Crameri et al. (2012)). In this approximation, there is a low-viscosity, low-density layer in the fluid (termed 'air' or 'water') above the free surface. Typically a free-slip boundary condition or the open boundary condition is used above the sticky air layer.
Examples in underworld2
Both the sticky air and free surface can be easily implemented in Underworld2. The examples are available by using UWGeodynamics module:
(1) "Stick air" method:
(2) Body-fitting method:
Free surface can be turned on using the Model.freesurface switch.
Model.freesurface = True
- Simple example,
- Case 1 from Crameri et al., (2012),
- Case 2 from Crameri et al., (2012),
- Rayleigh-Taylor Instability model from Kaus et al. (2010),
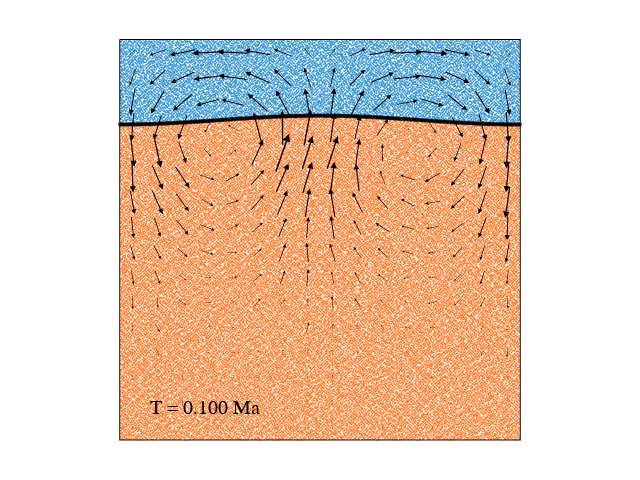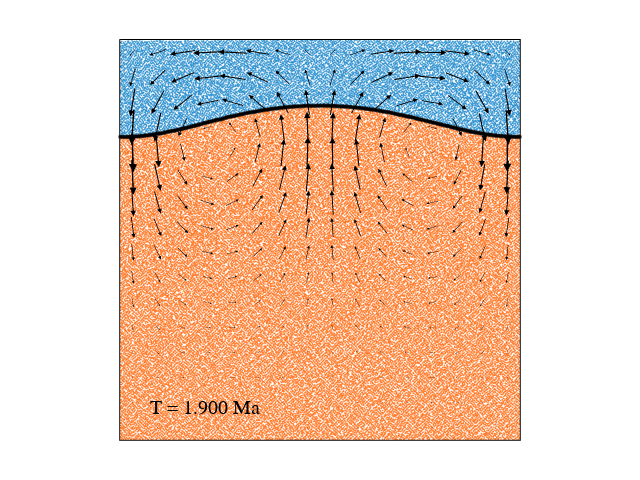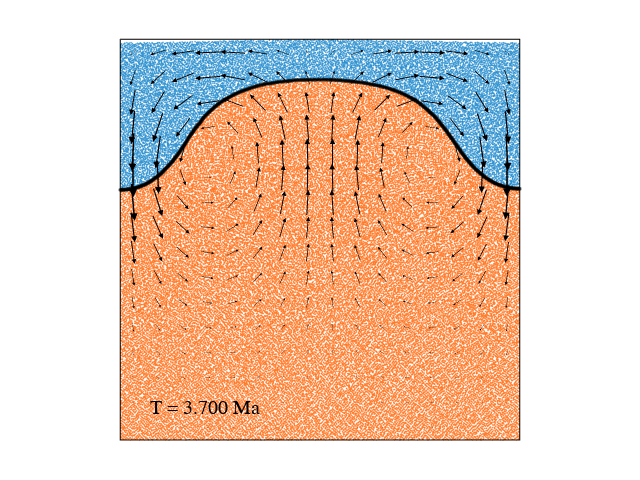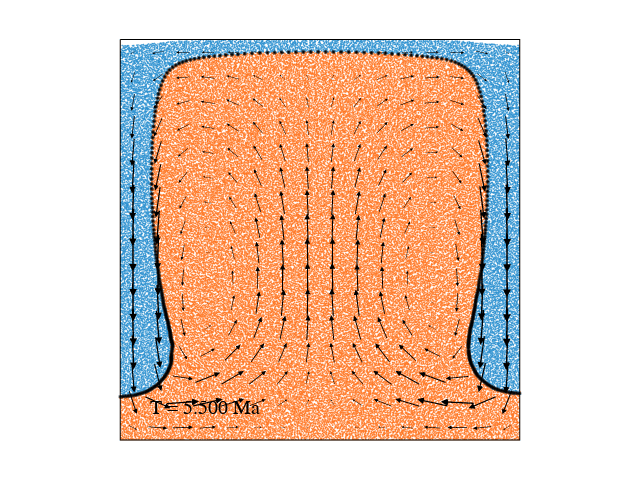
Limitations and stabllization methods
All of the approaches to free surface simulations have been subject to instability which has been variously termed a "sloshing instability" or the "drunken sailor effect" (Kaus et al., 2010). This instability, arising from the large density contrast typical at a free surface (the rock-air interface in the "sticky air" method), severely limits the maximum stable timestep for computations. Frequently, the maximum stable timestep is several orders of magnitude smaller than that for an equivalent model with free-slip boundary conditions. Stabilization methods (like FSSA from Kaus et al, (2010)) would be needed to solve that, while that's another story.

References
- Crameri, F., Schmeling, H., Golabek, G. J., Duretz, T., Orendt, R., Buiter, S. J. H., ... & Tackley, P. J. (2012). A comparison of numerical surface topography calculations in geodynamic modelling: an evaluation of the ‘sticky air’method. Geophysical Journal International, 189(1), 38-54.
- Kaus, B. J., Mühlhaus, H., & May, D. A. (2010). A stabilization algorithm for geodynamic numerical simulations with a free surface. Physics of the Earth and Planetary Interiors, 181(1-2), 12-20.
- Schmeling, H., Babeyko, A. Y., Enns, A., Faccenna, C., Funiciello, F., Gerya, T., ... & Van Hunen, J. (2008). A benchmark comparison of spontaneous subduction models—Towards a free surface. Physics of the Earth and Planetary Interiors, 171(1-4), 198-223.

Comments ()