ISMIP-HOM benchmark experiments using Underworld
Abstract
Numerical models have become an indispensable tool for understanding and predicting the flow of ice sheets and glaciers. Here we present the full-Stokes software package Underworld to the glaciological community. The code is already well established in simulating complex geodynamic systems. Advantages for glaciology are that it provides a full-Stokes solution for elastic–viscous–plastic materials and includes mechanical anisotropy. Underworld uses a material point method to track the full history information of Lagrangian material points, of stratigraphic layers and of free surfaces. We show that Underworld successfully reproduces the results of other full-Stokes models for the benchmark experiments of the Ice Sheet Model Intercomparison Project for Higher-Order Models (ISMIP-HOM). Furthermore, we test finite-element meshes with different geometries and highlight the need to be able to adapt the finite-element grid to discontinuous interfaces between materials with strongly different properties, such as the ice–bedrock boundary.
Characteristics of Underworld with regard to specific challenges in the modeling of ice flow
Underworld is designed to solve some of the special problems relevant to modeling geodynamic processes. Identical problems arise in the modeling of ice. Some of these challenges are as follows:
- the modeling of discontinuities in the material properties at layer boundaries, for instance, at the ice–rock and ice–air interfaces;
- gradients within the ice, for instance, due to strain softening or thermal effects;
- the tracking of the strain history;
- the often extreme spatial extent of the modeled systems;
- the very strong deformation of the material.
Underworld addresses these issues with the so-called material point method (MPM) (Moresi et al., 2003), which is closely related to the venerable particle-in-cell (PIC) method. MPM uses a Eulerian finite-element mesh in order to calculate the incremental development of the velocity field and other field variables, such as, temperature and pressure. In the MPM method, Lagrangian material points (“particles”) carry the density, viscosity, thermal conductivity and other relevant material parameters. The underlying mesh provides solutions for the incremental movement of the material points. The method is advantageous in the modeling of the emergence of structures (e.g., folding) or where very strong deformation is involved, as in the deformation across shear zones or near the base of an ice sheet. In MPM, the mesh does not carry any history information other than deformation of the boundary and therefore can be re-meshed at any time as required and without loss of accuracy.
There is an unavoidable smoothing which comes from the coarseness of the computational mesh relative to the material point density (Moresi et al., 2003). While material boundaries are represented by a continuous interpolant on the grid, they are necessarily discrete in the case of particles. This can lead to fluctuations in the solution close to sharp rheological or mechanical boundaries (Fig.1 and 2; Yang et al., 2021), for instance, at the interface between ice and underlying rock. In the ice itself, a change in mechanical parameters is usually more gradual and is controlled, for example, by the temperature gradient.

Fig.1 (a) Rectangular mesh. (b) Structurally conforming mesh, with increased resolution at the ice–rock interface. (c) Mesh perfectly fits the rock surface. Blue: ice. Red: bedrock
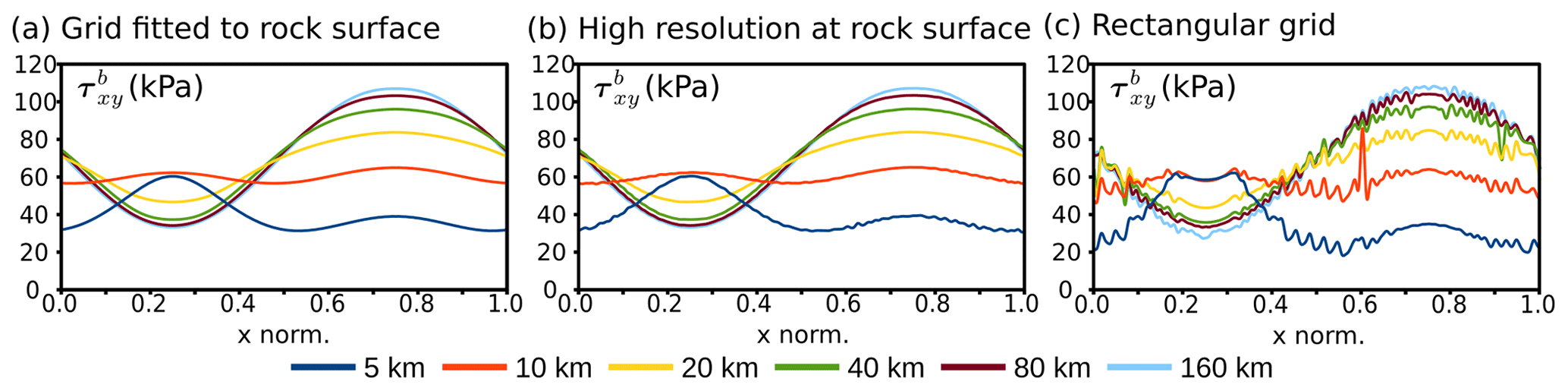
Fig.2 The basal shear stress (in kPa), calculated on (a) a grid fitted to the rock surface, and (b) a structurally more conforming grid, which increases mesh resolution at the rock surface and (c) a rectangular grid.
Another complication in the numerical modeling of ice flow is the highly anisotropic behavior of ice, created by the near-orthotropic properties of the ice crystal. The possibility to model anisotropic flow is built into Underworld (Mühlhaus et al., 2004). Like any other local material property, the orientation of the anisotropy can be stored on the particle level. In the case of isotropic ice, the flow field is controlled by the underlying topography. Hence the hill on the left acts as a bottleneck for the ice flow, and the hill sides funnel ice in and out of the bottleneck region (Fig3b). In the case of the anisotropic ice, the flow is strongly controlled by the inherent anisotropy and far less by the bedrock topography (Fig.3c). The flow field is internally subdivided into a fast-flowing upper part and slow-flowing “dead ice” in the lower part. Decoupling of the shallow and deep ice develops because the anisotropy facilitates shear along the horizontal basal planes.
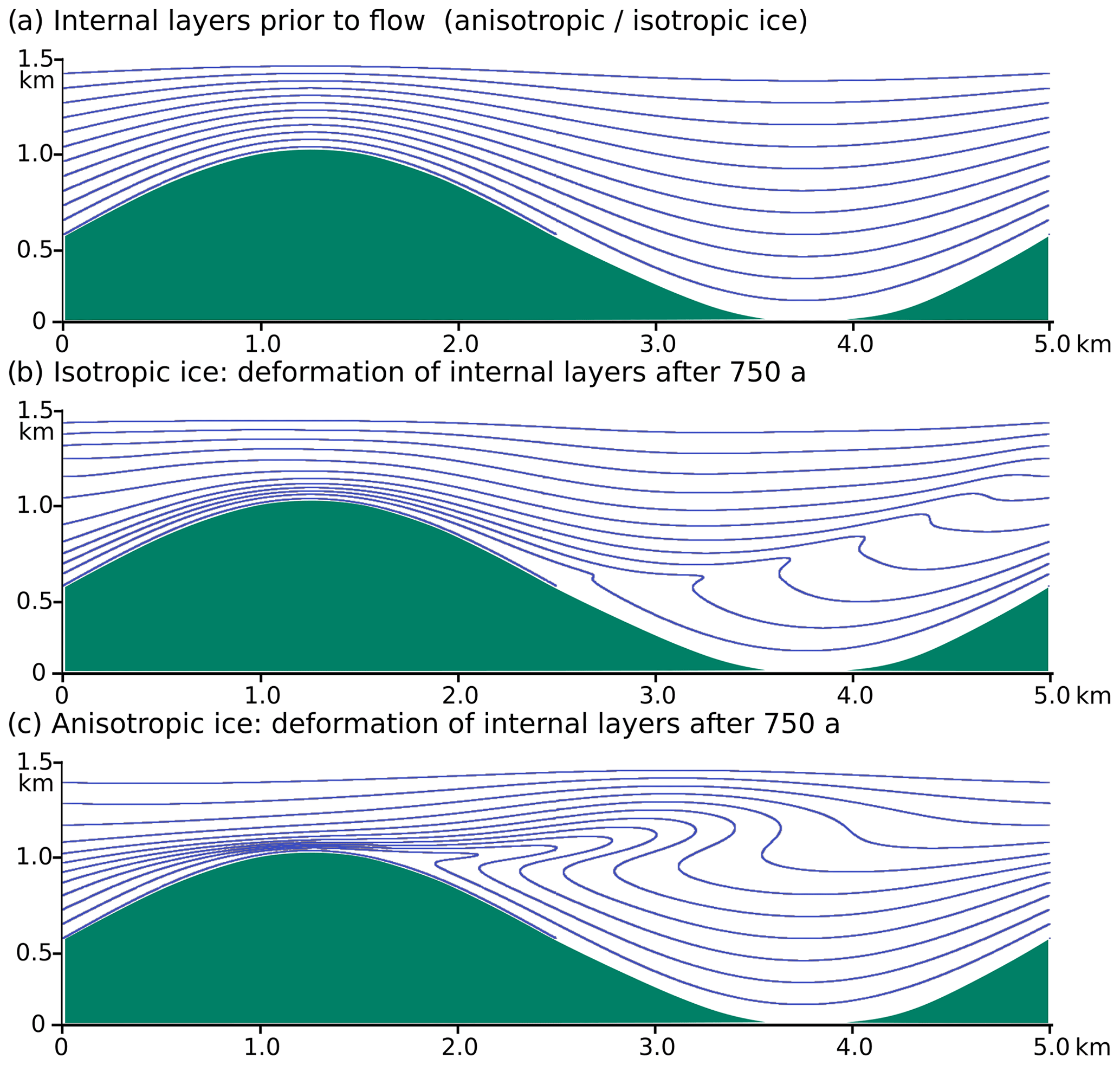
Fig.3 Marker lines prior to (a) and after 750 years of flow of (b) isotropic and (c) anisotropic ice. The axial plane of the resulting shear fold in isotropic ice mimics the bedrock topography, while it is controlled by shearing along a horizontal shear zone in the case of anisotropic ice. Green: bedrock, flow to the right.
Underworld offers a variety of possible solvers, including the well-known MUMPS, LU and multi-grid methods. We have carried out brief comparative precision tests with these solvers and could not find any difference in precision to the standard solver which is based on the multi-grid method. We recommend MUMPS for 2D models and multi-grid for 3D models.
Benchmarks
The Ice Sheet Model Intercomparison Project for Higher-Order Models (ISMIP-HOM; Pattyn et al., 2008, and Supplement or https://frank.pattyn.web.ulb.be/ismip/welcome.html, last access: 30 May 2022) provides tests for the comparison of computational ice-sheet flow models for different purposes. “Higher-order” here refers to models that go beyond the shallow-ice approximation (SIA) up to full-Stokes solutions (as Underworld does). The comparisons between Underworld and the ISMIP-HOM results are available online https://doi.org/10.5194/gmd-15-8749-2022-supplement. Here is one of the examples shown with jupyter notebook Exp_B_2.ipynb. All the python scirpits used to run models are avaibalble https://doi.org/10.5281/zenodo.7384424.
The related study has been published in the journal Geoscientific Model Development by Sachau et al., 2022.
References
Sachau, T., Yang, H., Lang, J., Bons, P. D., and Moresi, L.: ISMIP-HOM benchmark experiments using Underworld, Geosci. Model Dev., 15, 8749–8764, https://doi.org/10.5194/gmd-15-8749-2022, 2022.
Moresi, L., Dufour, F., and Mühlhaus, H.-B.: A Lagrangian integration point finite element method for large deformation modeling of viscoelastic geomaterials, J. Comput. Phys., 184, 476–497, https://doi.org/10.1016/S0021-9991(02)00031-1, 2003.
Mühlhaus, H.-B., Moresi, L., and Cada, M.: Emergent Anisotropy and Flow Alignment in Viscous Rock, Pure Appl. Geophys., 161, 2451–2463, https://doi.org/10.1007/s00024-004-2575-5, 2004.
Pattyn, F. and Payne, T.: Benchmark experiments for numerical Higher-Order ice-sheet Models, https://frank.pattyn.web.ulb.be/ismip/welcome.html (last access: 30 May 2022), 2006.
Yang, H., Moresi, L. N., and Mansour, J.: Stress recovery for the particle-in-cell finite element method, Phys. Earth Planet. Int., 311, 106637, https://doi.org/10.1016/j.pepi.2020.106637, 2021.

Comments ()