Stress recovery in Underworld

Issues with intra-element discontinuities in PIC-FEM

The classical finite element method (FEM) has been widely used to simulate diverse problems in engineering. Unlike most engineering problems, geological simulations are dominated by emergence of geometrical structures due to the non-linear processes involved. For the structurally conforming FEM meshes, the large deformations result in distorted meshes, which often require repeated re-meshing in computation. The particle-in-cell (PIC) method allows Lagrangian material particles to move in a background Eulerian mesh. Those particles carry the density, composition, viscosity, etc., while the unknowns are solved at nodes of the mesh.

In the tectonic-modelling problem, interfaces typically represent boundaries between materials of different viscosity (effective viscosity in the case of a visco-elastic problem) or the location of a shear-band with distinctive constitutive properties from the intact material. A viscosity jump within one element may give rise to errors more than two orders of magnitude larger than where material interfaces align with element boundaries. This viscosity jump can also significantly degrade the convergence properties of numerical solvers. For modelling long-term geological problems, the stress artifacts could dissipate this error to historical evolution with non-linear processes.

Stress Smoothing methods

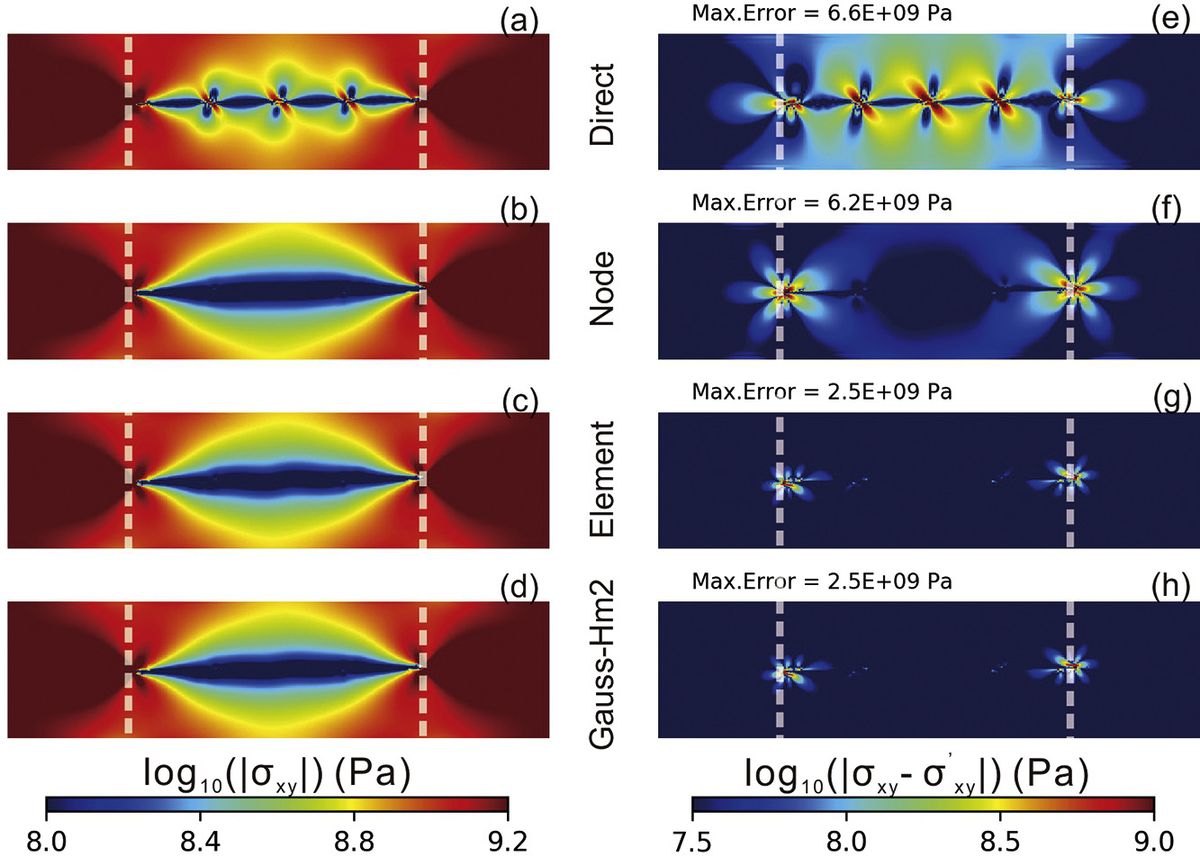
We examine the effectiveness of several smoothing methods in eliminating spurious stress fluctuations within the framework of Underworld. The smoothing methods we test can be conveniently implemented and efficiently run with Underworld. We first introduce two post-processing methods (projection function: type0 and type1) available in Underworld that are used to compute a smooth nodal stress or strain rate field, and then describe three pre-processing solutions that can be used to mitigate errors associated with the mesh not conforming to the interfaces: (1) a node-based method using the element shape functions, (2) an element-based averaging method, and (3) a Gaussian-quadrature-point based method using the distance weighted averaging.

Additionally, we further compare them with the classical stress recovery technique that reconstructs continuous stresses on specified patches based on nearby super-convergent points (SPR) (Zienkiewicz and Zhu,1992a,1992b). The SPR method was designed for cases without the internal structure in the element and is thus not intended to alleviate the problem caused by mixed-material elements. Each method is tested against analytic solutions for models that are relevant to geological problems. We also discuss how best to combine the various pre- and post-processing methods in “real” modelling situations. To be comparable with previous studies, the accuracy and convergence rate in the $L_2$ norm for the global model scale are provided. Additionally, we discuss the local maximum error, which is not addressed in previous studies but is of importance for geological problems such as shear band development where there is a non-linear feedback that can be sensitive to mesh-dependent errors.

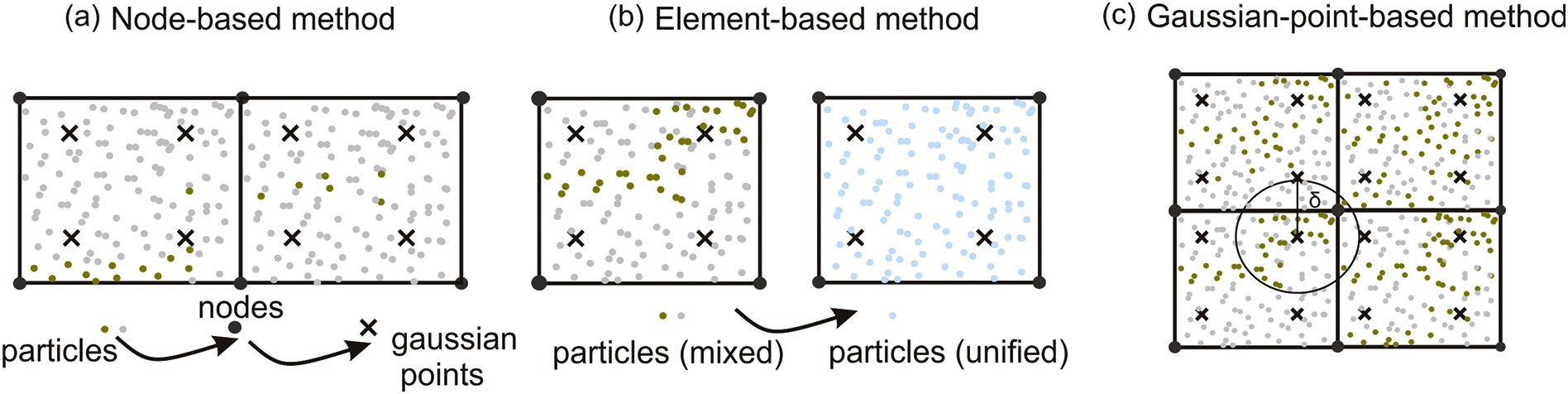
(a) The node-based method first projects reciprocals of particle viscosities to the mesh nodes, and then interpolate the reciprocals of node values to the Gaussian quadrature points. (b) The element-based method first locates the cells that contain different viscosities, then replaces the viscosities in the mixed-material cells with harmonic mean value of the materials involved. (c) The Gaussian-quadrature-point based method directly projects those particles that are within a distance of δ to the Gaussian point. The detailed description of the methods and the efficiency of different methods in recovering stresses are published in the Journal Physics of the Earth and Planetary Interiors by Yang et al., 2020. Implementation of these methods in Underworld can be found in GitHub and the live model, which also includes the post-processing code dealing with the error measurement.

References

Yang, H., Moresi, L.N. and Mansour, J., 2020. Stress recovery for the particle-in-cell finite element method. Physics of the Earth and Planetary Interiors, p.106637. (https://doi.org/10.1016/j.pepi.2020.106637)

Zienkiewicz, O.C. and Zhu, J.Z., 1992. The superconvergent patch recovery and a posteriori error estimates. Part 1: The recovery technique. International Journal for Numerical Methods in Engineering, 33(7), pp.1331-1364. (https://doi.org/10.1002/nme.1620330702)

Zienkiewicz, O.C. and Zhu, J.Z., 1992. The superconvergent patch recovery and a posteriori error estimates. Part 2: Error estimates and adaptivity. International Journal for Numerical Methods in Engineering, 33(7), pp.1365-1382. (https://doi.org/10.1002/nme.1620330703)