Stripy 2.0 released

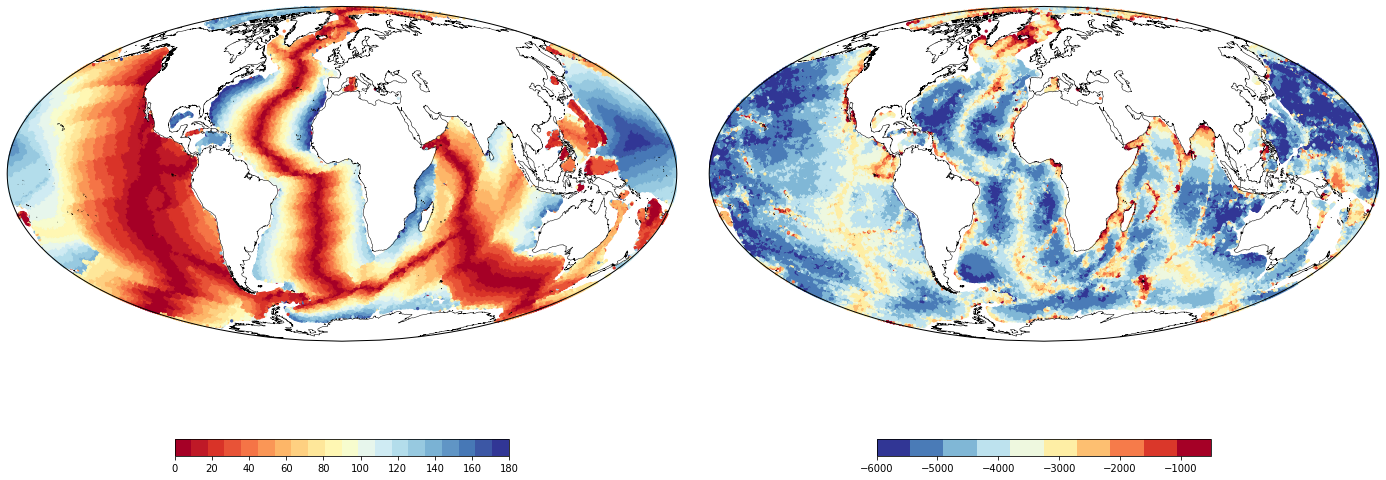
We've been busy creating the next major release of Stripy. To refresh your memory, Stripy is a Python tool for triangulating scattered points either in Cartesian coordinates or on the sphere. It wraps a bunch of Fortran codes in a neat, object-oriented Python interface that can be used for many geographical applications.

What's new?

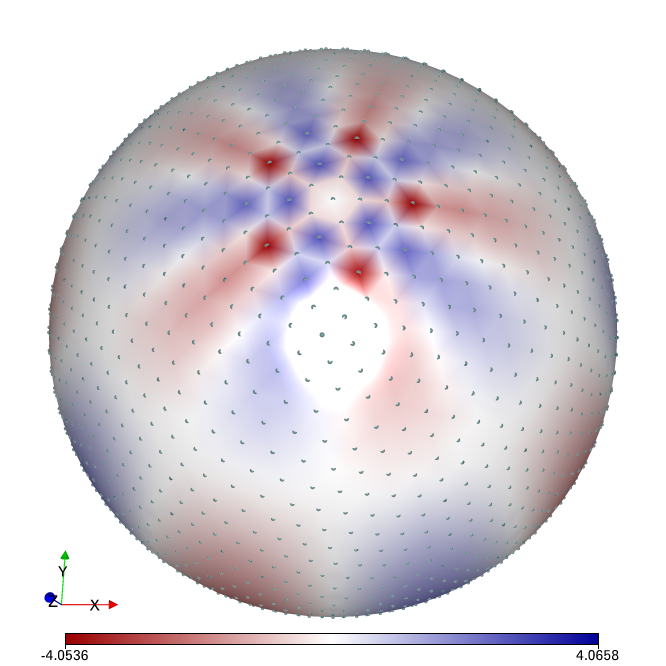
Spline tension - a lot of data transformations in Stripy are underpinned by cubic splines (e.g. interpolation, derivatives, smoothing). In v2.0 you can now add spline tension which avoids overshoot / undershoot artefacts. The most visible improvements are in accuracy of derivatives at points along the boundary and extrapolation of data beyond the boundary of a mesh.

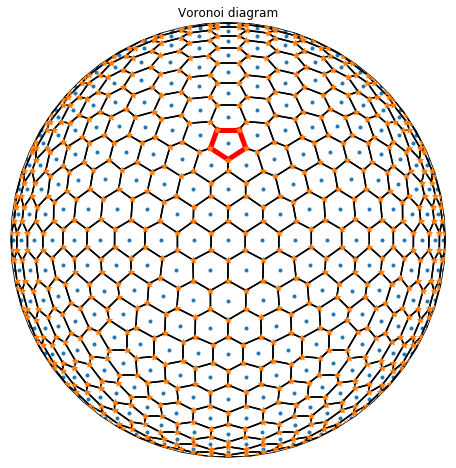
Voronoi diagram - the Voronoi diagram is the dual of a Delaunay triangulation. For every triangle in the mesh, there is a voronoi point which lies at an equal radius from each node. The diagram is constructed by connecting up the voronoi points from each neighbouring triangle.

Other notable new features include:

• a new equispaced elliptical mesh in Cartesian coordinates
• central area node weights for any mesh
• efficient evaluation of second derivatives in Cartesian coordinates
• better documentation, LGPLv3 license, and other small bug fixes

You can install the latest release of Stripy with pip

pip install stripy

or Conda:

conda install -c underworldcode stripy

Make Stripy better!

We welcome contributions to the code. If you want to add something you think is missing in Stripy, submit a pull request and if it looks good we'll merge your changes. Check out our contribution guidelines for more details.