Scaling in Underworld
To test scalability we run weak scaling tests on various HPC machines to check the numerical framework remains robust when pushing for higher fidelity models.

To date weak scaling tests have been run on two of the largest computers in Australia: Gadi (NCI) and Magnus (Pawsey).
Here we present the results of those tests and discuss:
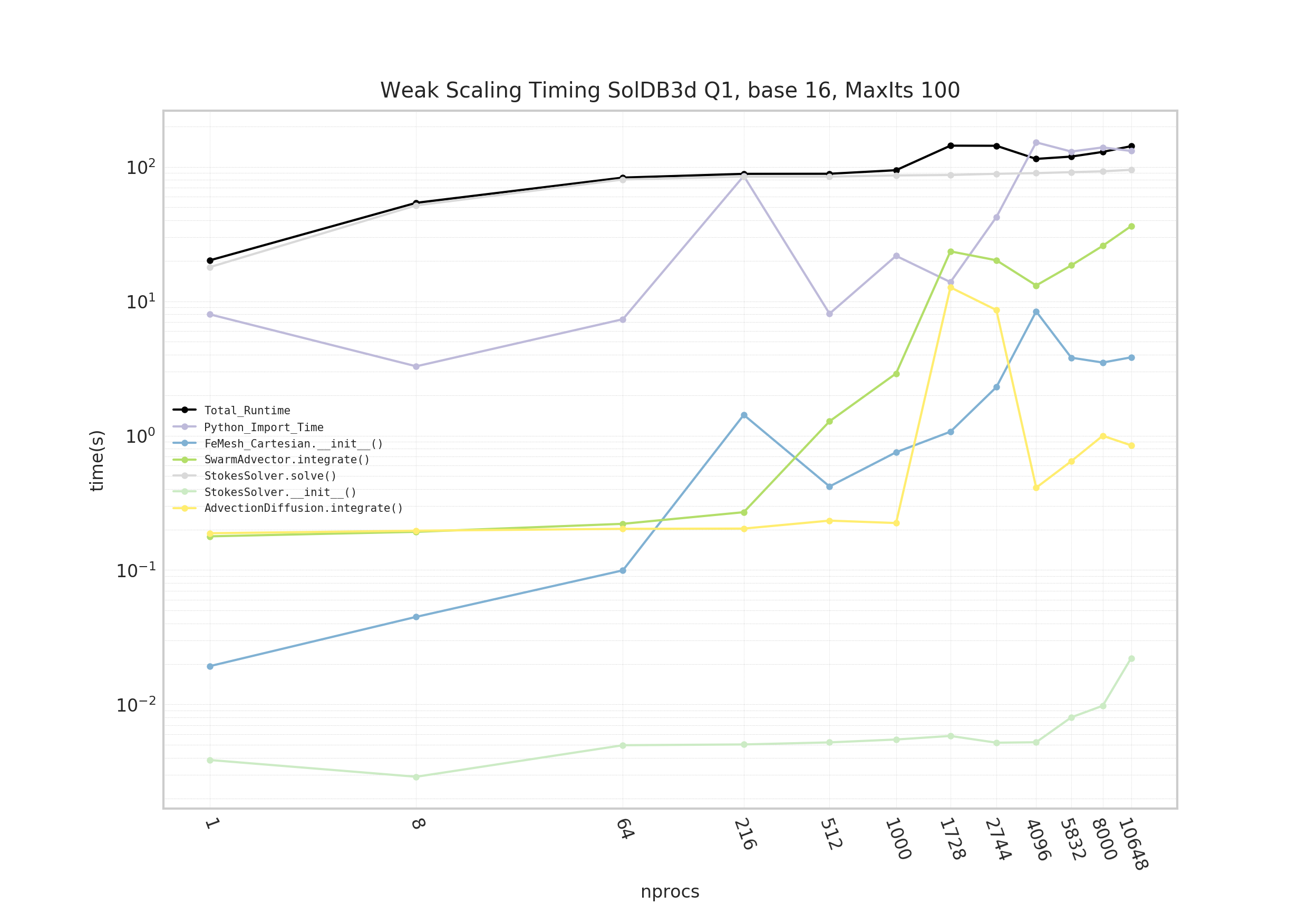
Gadi: Weak scaling - SolDB3D Q1
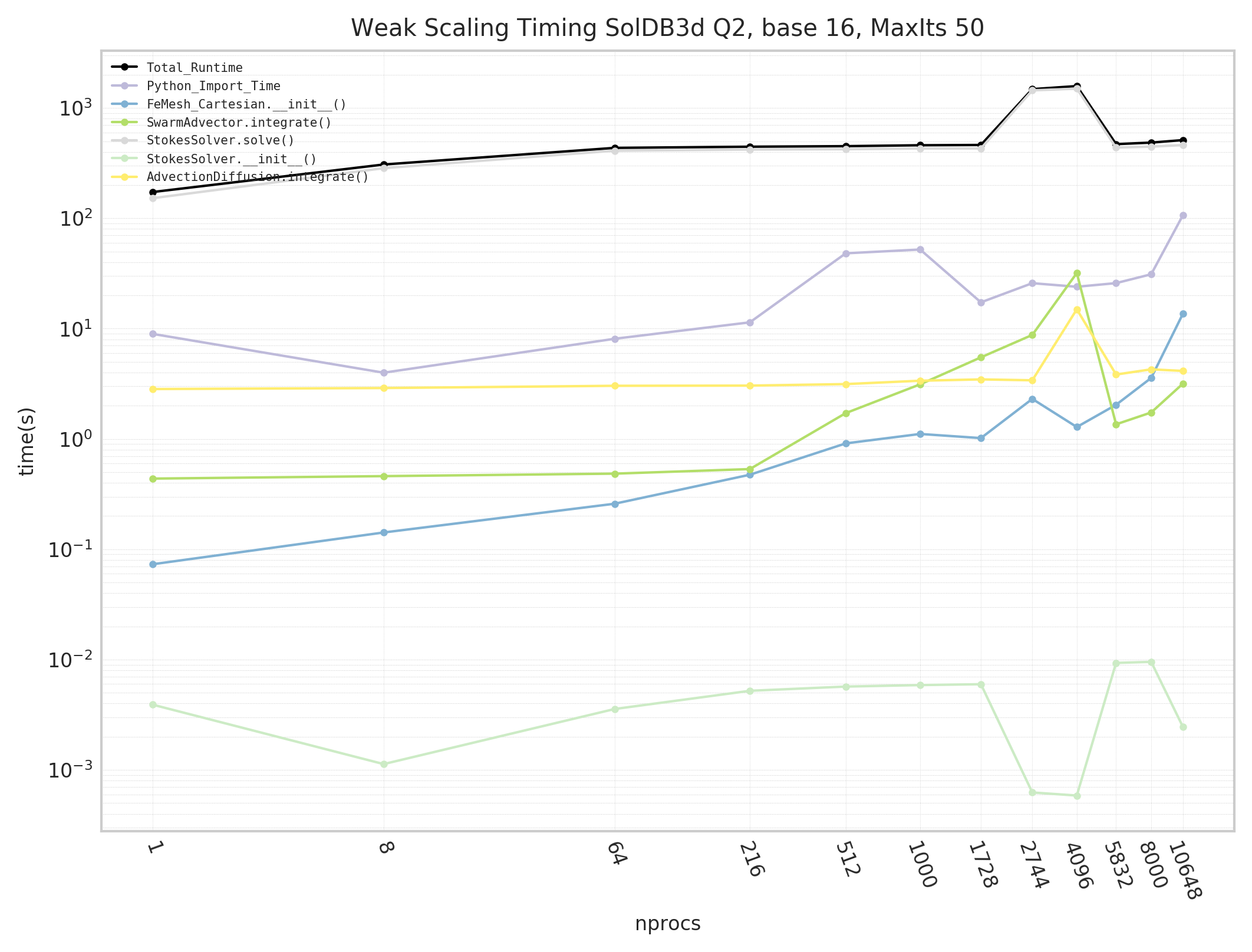
Gadi: Weak scaling - SolDB3D Q2
Magnus: Weak scaling - SolDB3D Q2 - v2.10 vs v2.9
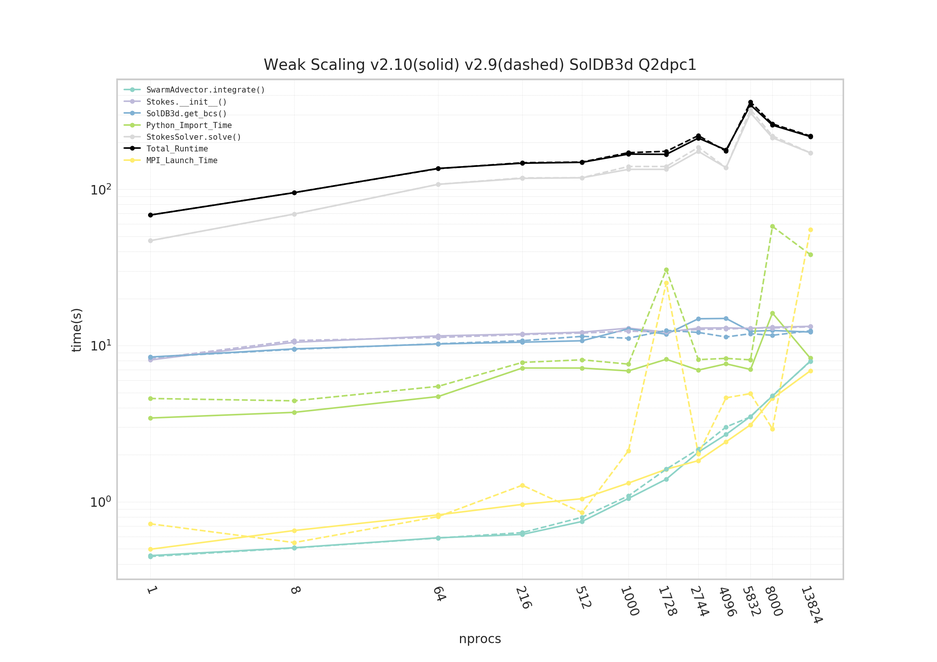
Underworld's Gadi installation is setup as a "bare metal" install, i.e. all code and dependencies are natively compiled onto Gadi's filesystem. However Magnus utilises Underworld's custom prebuilt docker via singularity containerisation.
Generally we see Underworld can scale to beyond 10k CPUs on both Gadi and Magnus. Wonderful!
It is noticeable that the Python_Import_Time scales more erratically on all Gadi runs rather than Mangus runs. Indeed it has been observed that some Gadi jobs, 500+ CPUs, fail to even start.
It is believed this issue is related to Underworld's (many) Python modules being read concurrently from Gadi's filesystem, overloading the filesystem with metadata operations and blocking IO. While on Magnus all Python modules are available to every CPU via the docker container and Python_Import_Time scales consistently.
The Underworld development team are continuing to work with the Gadi system admin to overcome this Python_Import_Time issue.
The analytic solution SolDB3D used as the reference model is based on the work by Dohrmann, C & Bochev, Pavel. 2004 [1], for the implementation details of of SolDB3D in Underworld see here
[1]: Dohrmann, C & Bochev, Pavel. (2004). A stabilized finite element method for the Stokes problem based on polynomial pressure projections. International Journal for Numerical Methods in Fluids. 46. 183-201.




Comments ()